Introducing the GGT-NN

Note to present-day readers: The use of the word "transformer" in this post, and in the corresponding ICLR paper, is unrelated to the now-popular Transformer architecture introduced in the paper "Attention is all you need", which was released shortly after this post.

Recently, I submitted a paper titled "Learning Graphical State Transitions" to the ICLR conference. (Update: My paper was accepted! I will be giving an oral presentation at ICLR 2017 in Toulon, France. See here for more details.) In it, I describe a new type of neural network architecture, called a Gated Graph Transformer Neural Network, that is designed to use graphs as an internal state. I demonstrate its performance on the bAbI tasks as well as on some other tasks with complex rules. While the main technical details are provided in the paper, I figured it would be worthwhile to describe the motivation and basic ideas here.

Note: Before I get too far into this post, if you have read my paper and are interested in replicating or extending my experiments, the code for my model is available on GitHub.

Another thing that I've noticed is that almost all of the papers on machine learning are about successes. This is an example of an overall trend in science to focus on the positive results, since they are the most interesting. But it can also be very useful to discuss the negative results as well. Learning what doesn't work is in some ways just as important as learning what does, and can save others from repeating the same mistakes. During my development of the GGT-NN, I had multiple iterations of the model, which all failed to learn anything interesting. The version of the model that worked was thus a product of an extended cycle of trial and error. In this post I will try to describe the failed models as well, and give my speculative theories for why they may not have been as successful.

Inspiration

Back in April, as the school year was drawing to a close, I started thinking about other interesting AI research problems I could tackle. At the time, I had been reading a bunch of different AI research papers.

One particularly impressive paper I had read was Neural Turing Machines by Graves et al., which was a powerful demonstration of the ability of sophisticated neural networks architectures to learn complex tasks. In it, the authors describe training a recurrent controller network to access differentiable external memory using an attention mechanism. The model successfully learned to utilize the memory in a meaningful way and was able to essentially discover algorithms for solving the tasks it was given.

I also read a bunch of work from Facebook AI Research, including End-to-End Memory Networks and Towards AI-Complete Question Answering: A Set of Prerequisite Toy Tasks (also known as the bAbI task dataset). Both of these papers are about question-answering tasks, in which a neural network is fed information about the world and then is given questions in textual format that it must learn to answer based on the information. Memory networks were one approach to this problem: each fact about the world was stored in a differentiable "memory" matrix, and then the model selected particular facts out of the memory (using attention) to try to answer the query. While this works well for solving some tasks (like asking what room someone is in after being told the locations of everyone) it does not work well for complex tasks which require multiple facts. For instance, memory networks were not able to easily learn to solve pathfinding tasks, since that required an awareness of the connectivity of multiple rooms, not just of single relevant facts.

Sample statements from the bAbI task dataset.

At this point I started thinking about how one might approach solving that kind of complex problem. I realized that, as a human, if I were asked to find a path between multiple rooms, I would not think about textual facts. In other words, I would not think "OK, so I want to get from the bedroom to the kitchen, and the bedroom is adjacent to the hallway, and the hallway is adjacent to the other bedroom and also to the living room, and the living room is adjacent to the kitchen and to the bathroom, so I need to go to the hallway and then the living room and then the kitchen". Instead, I would solve the problem visually. I'd picture the whole floor plan, and determine what the shortest path is using the visual distance between things.

Based on this, I started thinking about how a neural network might do something similar. The important thing, I realized, was that the structure of my knowledge was NOT a set of facts; it was a complex web of connections and associations (that happened to have a nice visual representation). In essence, my knowledge could be better represented by a graph than by a list of facts.

Furthermore, all sorts of knowledge seemed to fit a graphical structure. Relationships between people can be encoded with edges to represent relationships, and nodes to represent people. Places can be represented as nodes, with paths between them as edges. And many data structures have a natural graphical representation, such as linked lists, sets, and trees.

After looking for prior work in this area, I found Gated Graph Sequence Neural Networks, by Li et al., which described a recurrent architecture that operated on graphical input. For each sample in the training data, a graph structure is built. Then each node is given an internal state, and nodes are allowed to exchange information between each other across edges and update their states as in a recurrent neural network. However, although this model works well for answering a query based on a known graph structure, it does not actually help generate the graph. That part must be done in advance through preprocessing of the dataset. I decided that I would try to work on a method that would enable the graph itself to be built and modified by the network.

First attempt: Differentiable graph + recurrent controller

My first attempt at doing this was based heavily on the Neural Turing Machine model. The bulk of the computation was done by a recurrent controller, implemented with LSTM cells. The controller would interface with a differentiable graph structure using a set of read-write "selections", one of which was active at a time.

To make modifications to the graph, the controller would output one of a set of commands, such as "move the active selection to a particular node", "move the active selection across an edge", "copy one selection into a different selection", "make a node and point the active selection at it", "make an edge between the two nodes connected by two selections", etc.

The graph structure and the selections were also "fuzzy" in order to make the process differentiable. Each selection had a different "selection strength" for each node, which was a value between 0 and 1. If the controller could not decide between two commands (i.e. choosing two commands with 0.5 confidence each), the final selection would be a mixture of the selections produced by each command, and thus would half-contain some nodes (with strength 0.5). Furthermore, the actual nodes and edges themselves had fuzzy strengths, allowing a node to be partially created.

After implementing this model, and fixing a plethora of numerical stability issues, I was rewarded with a complete failure of the model to learn anything useful at all. The model consistently ended up "blurring out" the selections: the controller wouldn't commit to any particular choice, and would end up doing everything with a low confidence. As a result, all of the selections ended up weakly containing every node, and the resulting graph was just a tangle of low-strength nodes connected by useless edges.

In hindsight, there were many reasons why this model did not work well. First of all, the individual operations were too complex. If one wanted to make a single node connected to another node, many steps were required: first creating the node, then selecting the second node, then creating an edge between the two. Secondly, there was too much potential for "blurring". At pretty much every step, it was possible for the selection to break down and weakly select everything. Finally, there were too many equivalent ways to achieve the same solution, by creating nodes in a different order or using different selections.

These combined to essentially eliminate the influence of gradient descent on the solution. Since there were multiple possible ways to reach the same solution, the model did not learn to strongly choose any particular set of actions. And then one the selections were all blurred, no individual change in the network parameters would be enough to bring the graph back to the correct state, since the correct solution required multiple steps with non-blurred selections.

Second attempt: Reinforcement learning and a discrete graph

At this point, I thought that I could resolve many of the problems of the previous model by ensuring that everything was always discrete, i.e. that selections always either contained nodes or didn't, and only one action was taken at each step. To accomplish this, I turned to reinforcement learning.

The overall construction of the network was the same as before. However, instead of using a differentiable graph and partially executing commands, I sampled a particular command at each step and ran that command on the graph with full strength. I then constructed a cost function that measured the difference between the correct graph and the graph made by the network. The model was then trained to make the choices that produced a graph with a lower cost.

To implement this, I used OpenAI's rllab library. I then ran it using a variety of possible optimization methods, including TRPO and REINFORCE. Unfortunately, this also failed to produce any useful results. The network could not learn the complexity of the tasks, and made mostly random choices. Trying to improve the performance of the network using different optimization methods cause the network to output NaN results and destabilize the training procedure.

The main problem with this model was the enormous size of the state space. At every step, the controller had to choose between at least 50 different actions it could take. And the only way to produce the correct graph was to execute a sequence of multiple specific actions (usually at least 3 or 4). Pretty much any other sequence of actions produced a bad graph and was worth no reward.

The correct sequences were thus very rarely observed, and as a result, the network was penalized for pretty much anything it did. This made it very difficult to learn what the correct actions were at each step, making the overall model fail to perform correctly.

At this point, one idea I briefly entertained was to specifically "inject" sequences that produced the correct graph into the training algorithm, essentially biasing the sampling toward what would be correct. But this would be essentially equivalent to doing regular supervised learning of a sequence of actions, and would defeat most of the purpose of reinforcement learning. Furthermore, I did not have a transformation that would take a graph and produce a correct sequence to build that graph. And building one seemed to defeat the purpose of the entire network, since that was exactly what it was supposed to learn on its own.

Right around this time, I was getting busy with my research with the Intelligent Music Software team at HMC, which I described in my last major blog post. I had also become a bit discouraged with the graph model, and put it aside for a few weeks while I worked on some other things.

Insight: Bottom-up, distributed processing

The graph network kept bouncing around in the back of my mind, though. I had tried most of my ideas for fixing the problems of the current model, but had had no luck with any of them. I was pretty convinced that if I wanted to get the model to work, I would have to start from scratch, and abandon the core assumptions of my existing designs.

I started to think back to the design of the Memory Network and Gated Graph Sequence Neural Network models. And I realized something interesting about both. Both of them dealt with a large number of distinct elements, facts in the first case and graph nodes and edges in the second. But neither of them had a central controller! Instead, they used a bottom-up approach, and distributed the processing of the network across the individual elements.

In the memory networks, every fact got transformed into a "memory vector", and these vectors were all independently stored. Then, when formulating an answer to the query, every memory was checked simultaneously for relevance to the query, and information was extracted from the most relevant memories, weighted by relevance. There was no recurrent controller that moved between the memories and checked them in turn, accumulating information; instead the memories themselves dictated how information flowed out of them, and the output was combined at the architecture level.

Similarly, in the GGS-NN models, the nodes were the locations of the recurrent processing. Each node acted as its own instance of the network, and had an independent internal state that was modified according to information from adjacent nodes. There was no single recurrent controller here, either, and no selections used to extract information from the nodes. Instead, each node acted independently, and the behavior of the overall system was determined by the individual changes in each node. At the final output step, the states of all of the nodes were combined using attention in the same way as in the memory networks: every node's state was checked simultaneously for relevance, and information was extracted from the most relevant nodes, weighted by relevance.

As I thought about my earlier designs, I realized that pretty much all of my problems seemed to stem from the choices made by the controller: there were too many options, and the sequences of choices were too sophisticated. I realized that if i got rid of the controller entirely, and delegated the responsibility to the nodes themselves, I might be able to eliminate the problems that had plagued my earlier models.

Third and final attempt: The GGT-NN

In order to get rid of the controller, I needed to figure out a way of modifying a graph in a bottom-up fashion, so that it could be determined by the nodes themselves. But this was a nontrivial problem. Between two different graphs, any number of changes could need to be made, such as

• creating new nodes
• adding new edges
• removing old edges

(Note that, for simplicity, I did not allow removing old nodes, since the network could just learn to ignore any nodes that became irrelevant.) In addition, if the nodes were responsible for all of the state, there would also have to be mechanisms for

• updating the state based on new information
• propagating state information between nodes
• producing a single output

After thinking about this for a while, I realized that by performing these changes in a certain predefined sequence, it would be possible to make almost any adjustment to the graph:

1. Update the state for each node based on new information.
2. Propagate this updated state information between connected nodes.
3. Add any necessary new nodes.
4. For each pair of nodes, determine whether or not to create or remove any edge between those nodes, based on the states of each node.

This process can be seen as a series of transformations, each of which take in a previous graph and possibly some new information, and produce an updated graph. In particular, the transformations that I came up with and implemented were:

1. Node addition
2. Node state update
3. Edge update
4. Propagation (sharing information)
5. Aggregation (producing a single output representation from the whole graph, using attention)

Node addition is a bit tricky. Each of the nodes may have a say in what new nodes should be created (if there is already a node for Mary, for example, we wouldn't want to make a new one!). But no individual node seems like it should be responsible for creating the new nodes. Furthermore, we may want to make multiple nodes in the same timestep. The solution I ended up using was to have a GRU layer, whose input was a combination of the new information and an attention-based aggregate of the "opinions" of all of the existing nodes. That GRU would then output a sequence of new nodes and specify what type each should be. The GRU can output nodes with fractional strength, allowing partial creation of nodes and thus producing a differentiable transformation.

Node state updates are relatively simple, and are implemented identically to a Gated Recurrent Unit (GRU) update. The only difference is that every node has an independent state and is updated independently. In the paper, I also describe a more sophisticated version known as "direct reference update", in which each distinct type of node uses a different input vector based on the information relevant to that node, but otherwise the process is the same.

Edge updates are implemented using simple feedforward networks. In parallel, every pair of nodes is considered, and the states of both nodes are passed to a two layer network that determines whether an edge of each possible type should be created, removed, or left as it is.

Propagation and aggregation are implemented essentially identically to the propagation and output representation in GGS-NNs. The main difference in propagation is that it is explicitly performed using a neural network instead of just a matrix multiplication, and the strengths of nodes and edges are taken into account. The aggregation step is also similar, and was modified slightly to weight the information by the strengths of the nodes.

This final, distributed model ended up working very well. I was able to run it on all of the bAbI tasks, and it solved 18/20 of them with 95% accuracy or above. I also trained it to simulate both Rule 30 and any 4 state Turing machine.

I experimented with training the model with different levels of supervision. In one trial, I attempted to see if the model could learn the appropriate graph structure on its own based only on the requirement that it answer the query correctly, without being told what to produce. Unfortunately, this did not work. However, if I provided the model with the correct graph at each timestep and trained it to produce that graph, it would readily learn how to do so. I think this is a reasonable level of supervision, since for many tasks there is a very particular type of graphical structure that we want to use.

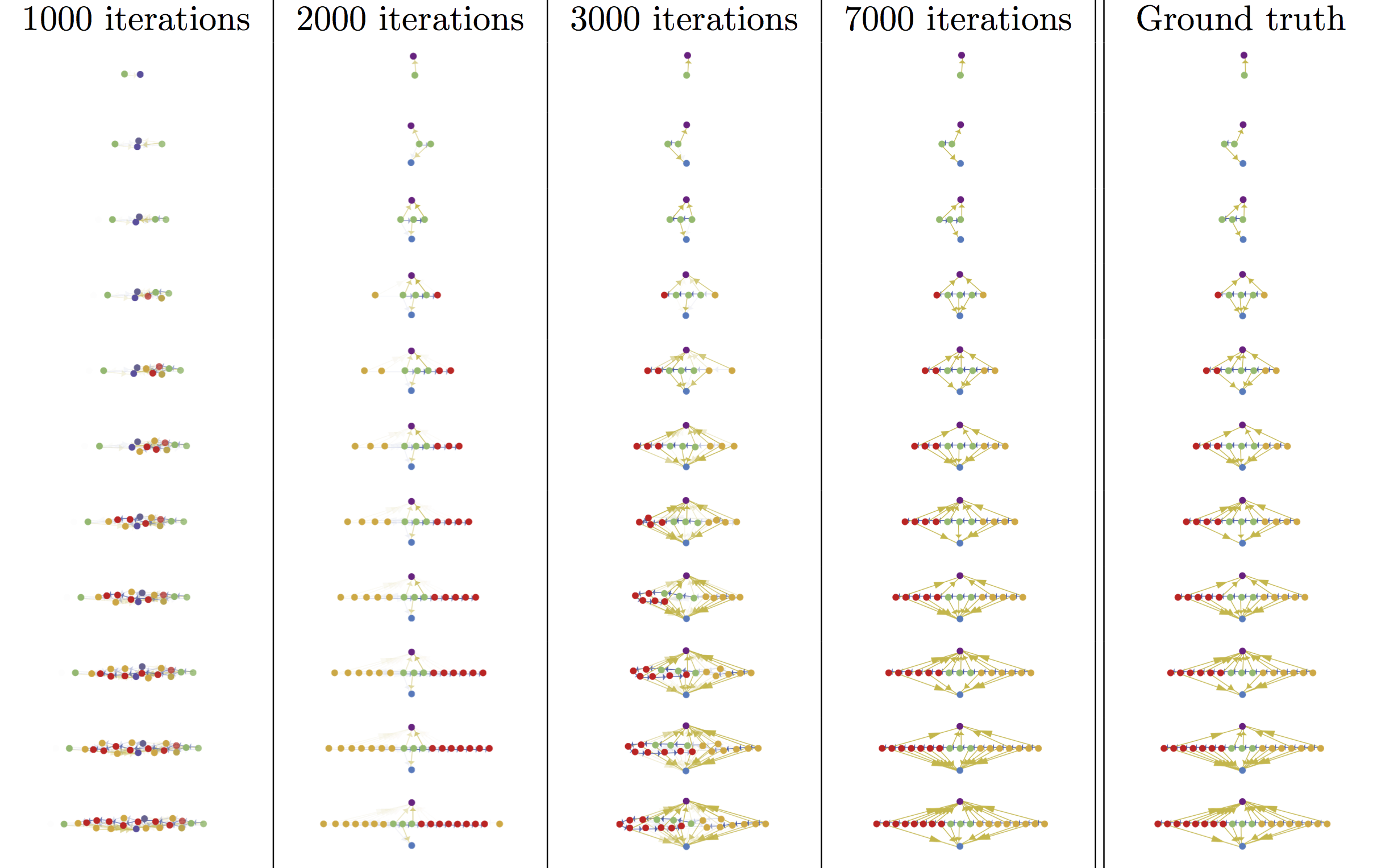
Here are some fancy pictures of the model at various stages in learning how to simulate the Rule 30 automaton. Coloring and position indicate the types of nodes produced by the network. Notice that at the beginning, it learns how many nodes to produce, but does not have the node types (colors) correct. Over time, it learns what to produce at what time, but still struggles with which edges to make until late in the training process. (Click the image for full resolution.)

Ultimately, I'm very happy with the results of the model. The GGT-NN model can successfully learn how to parse textual input and build a graph, and can discover rules underlying the behavior of complex graphical systems. Of course, there are a few disadvantages of the model:

• Every unique type of entity has to be represented by a different node type, and behaviors for each type have to be learned independently. So if there are a lot of possible values for something, it can be difficult to train.
• Since every edge between every node is considered at each timestep, and every timestep can add multiple additional nodes, the amount of processing grows very large very quickly for complex tasks (it is something like $O(n^3)$ in the length of the input).
• If multiple nodes are created at the same time, they cannot be of the same type, because then they are indistinguishable. This is as much a problem with the network as it is with the training method, because it is unclear how to determine a cost function for an incorrect graph if multiple nodes can look identical.

However, I'm sure that many of these can be overcome with future research, and even with these restrictions, it seems like there are many potential applications of the GGT-NN model. I'm excited to see how they get used!

Again, if you want to read my paper, which goes into the technical details of the model and the experiments, you can do so here. And if you want to see the code I used to run my experiments, it is all available on GitHub.