Discrete and Computational Geometry Projects
At Harvey Mudd, I'm taking a cool class called "Discrete and Computational Geometry", a special topics course taught by Professor Satyan Devadoss. It's a very interesting class. In lieu of normal problem sets, we instead do a bunch of group projects, each one very freeform. The basic instructions are "go make something related to this class". Here are a couple of the projects my group made:
Interactive Art Gallery
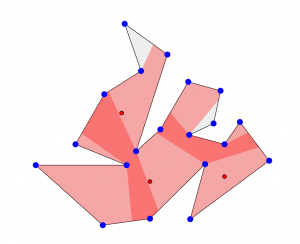
This project was about the Art Gallery problem, which asks what is the fewest number of guards that can guard a polygonal art gallery. We built a visualization to allow you to construct a polygon and place guards. It also computes a lower bound solution, which is guaranteed to have floor(n/3) guards for a polygon with n vertices. You can see it here.
Associahedron
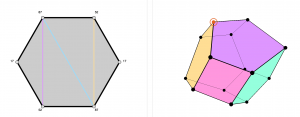
This project is a visualization of an associahedron, a polyhedron that corresponds to the triangulations of a polygon. There's some crazy math about associahedrons, and one cool property is that computing "area vectors" of a triangulated hexagon creates a geometric 3d associahedron that deforms continuously. Check it out here. (Update: Or read the multimedia exposition paper here for more details on what it happening.)
Fold and Cut
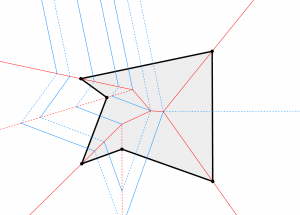
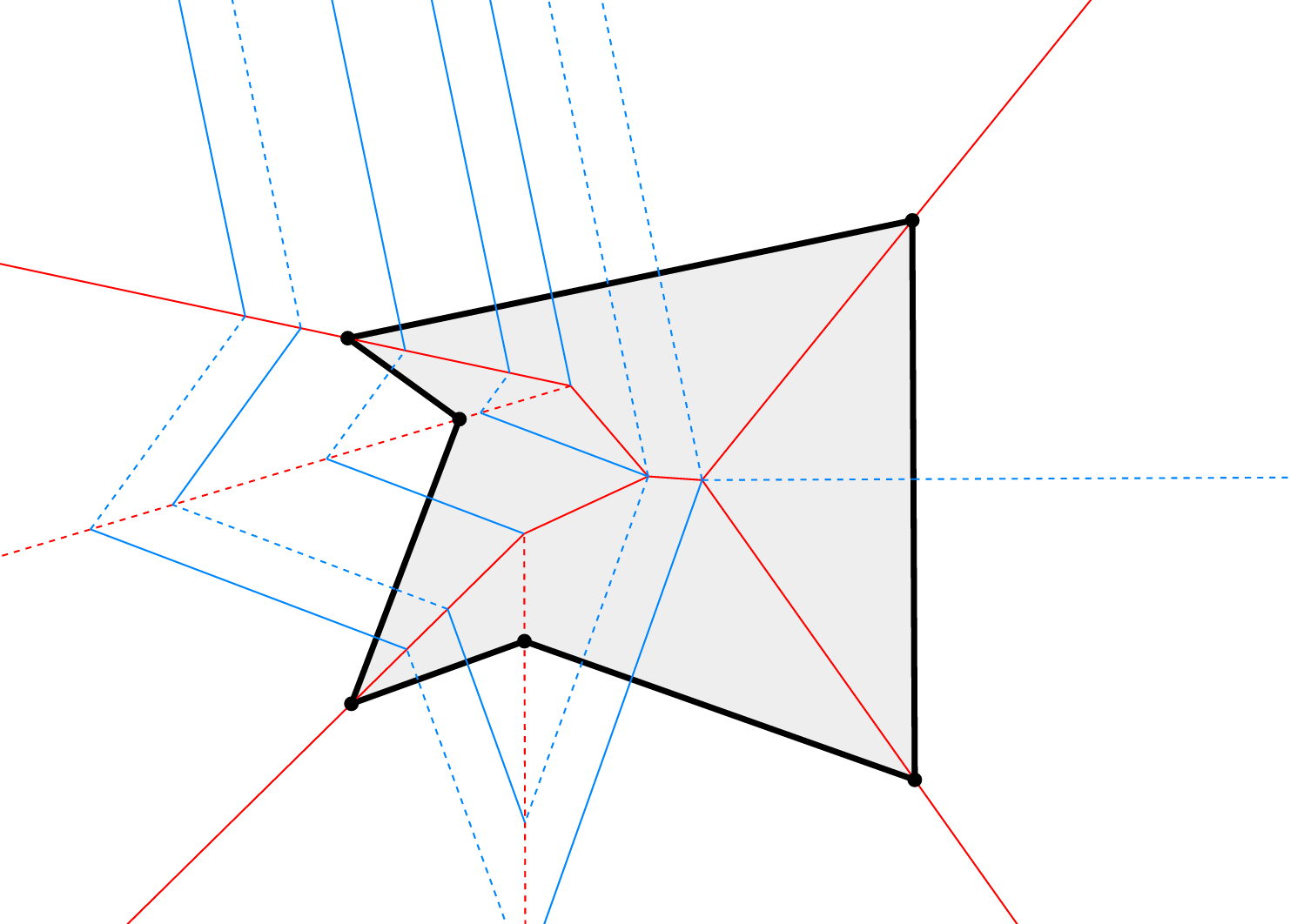
Finally, the Fold and Cut theorem states that any shape with straight sides can be cut out by folding a sheet of paper and then making a single cut. This was proved by Erik Demaine et al., and we implemented Demaine's construction to show how to fold and cut an arbitrary closed polygon. Try it out here.